NEGF formalism¶
The nextnano.NEGF tool is based on the non-equilibrium Green’s functions (NEGF) formalism (also known as the Keldysh, or Kadanoff-Baym formalism). This formalism allows to account for both quantum transport effects (i.e. coherent transport effects such as resonant tunneling), as well as scattering mechanisms.
In the NEGF formalism, scattering processes are described in terms of self-energies. Self-energies and Green’s functions are calculated in a self-consistent way, as both elastic and inelastic scattering processes are accounted within the self-consistent Born approximation (Figure 4.2.1).
Self-consistent solver¶
To found the steady-state solution, several equations needs to be solved self-consistently
The calculation of self-energies (i.e. the evaluation of scattering processes)
The Dyson equation to calculate the retarded Green’s function \(G_R\), from which the local density of states can be extracted.
The Keldysh equation to calculate the lesser Green’s function \(G^<\), from which the density matrix and the charge density can be extracted
The Poisson equation which relates the electrostatic potential to the charge densities
The figure Self-consistent solution algorithm below and above lasing threshold. shows the principle of the algorithm used to solve these equations self-consistently.
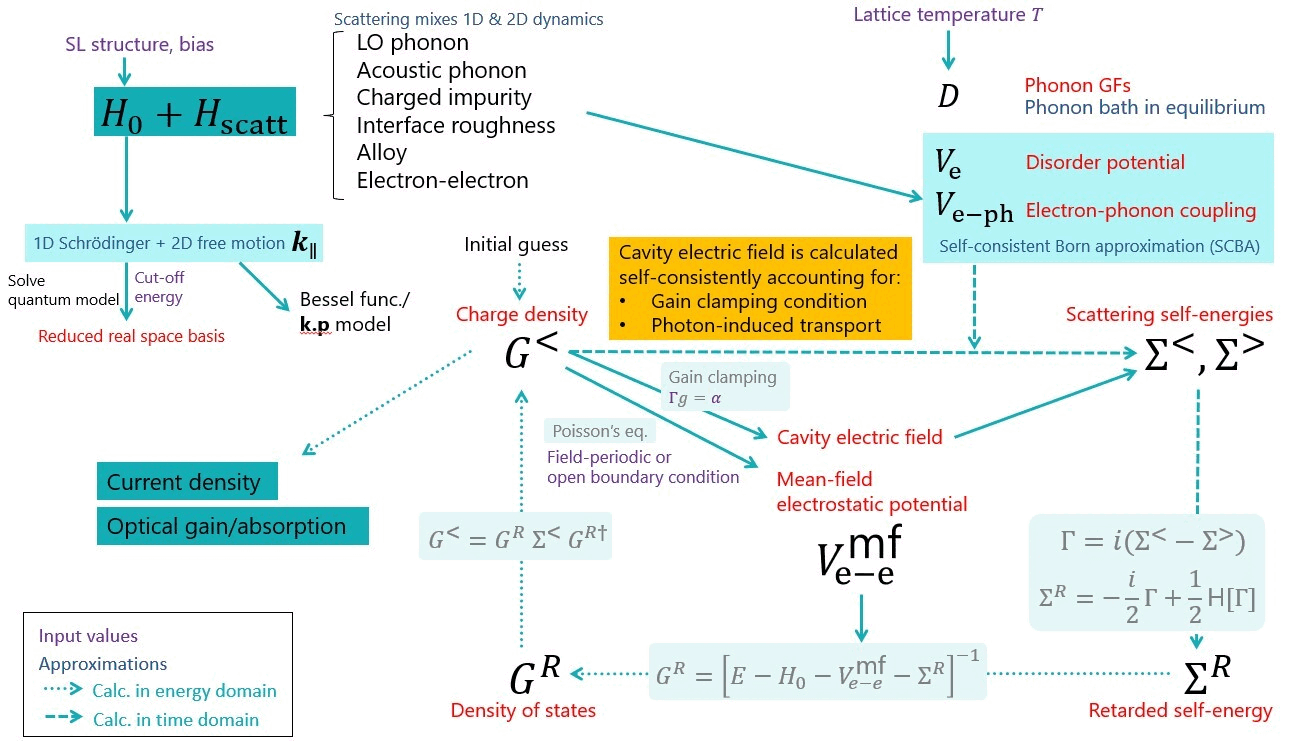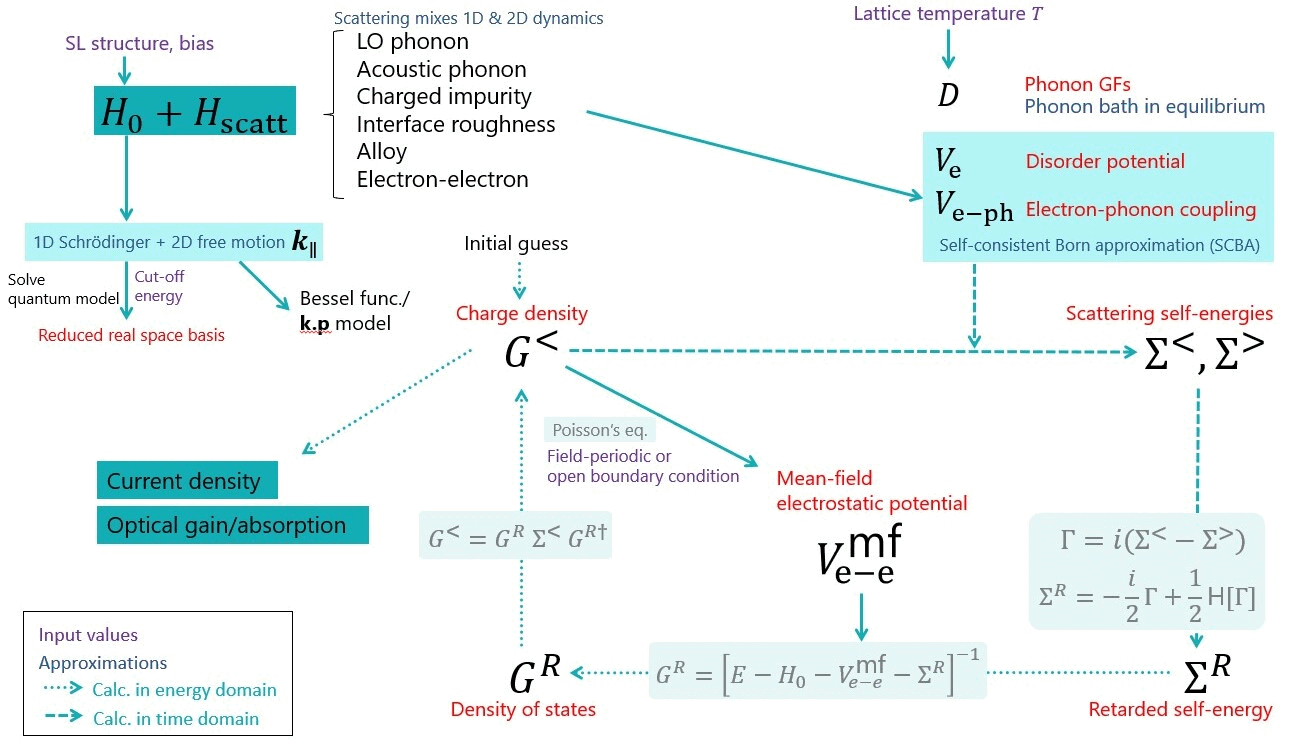
Figure 4.2.1 Self-consistent solution algorithm below and above lasing threshold.¶
At the beginning of the calculation, the one-dimensional Schrödinger equation is solved in real space. The energy levels (minibands in the case of periodic system) are selected by the energy interval specified in the input file (see Axial energy cut-off). The energy levels are transformed into a localized basis of modes which we call Reduced Real Space basis. These wave functions are then used as the basis of the Green’s functions and self-energies.
Secondly, the scattering coupling terms are calculated for each of the accounted mechanism (optical and acoustic phonons, charged impurities, interface roughness, alloy disorder, and electron-electron scattering).
Then, the Green’s functions and self-energies are calculated iteratively. Simultaneously, the mean-field electrostatic potential is calculated self-consistently via Poisson’s equation. Such iterations continue until Convergence is reached for the Green’s functions as well as for the calculated current.
After the convergence, the carrier and current densities are calculated from the Green’s functions. To gain more insights into analysis, the populations, density matrix, oscillator strengths are output in different bases.
The Optical gain/absorption spectrum is calculated if requested in the input file (see Gain{ }). In this case, an additional self-consistent routine can be used to calculate the linear response of the Green’s functions to an a.c. electromagnetic field perturbation.
Convergence¶
The NEGF self-consistent loop ends successfully if the relative difference between two consecutive iterations has reached ConvergenceValueGF for the lesser Green’s function and ConvergenceValueCurrent for the current density. If the convergence is not achieved, the iteration is terminated after NMaxIterations.
Note
Small values for the convergence values, together with sufficiently large NMaxIterations, will give the most accurate results.
Last update: 19/11/2024