Doping in semiconductors: Incomplete ionization
The input files used in this tutorial are:
1D_doped_bulk_Si_doping_sweep_Altermatt.in
IncompleteIonization_Altermatt_nextnano3.py
Table of Contents
Doping in semiconductors: Incomplete ionization in semiconductors (Altermatt model)
This tutorial tries to reproduce Fig. 5 of [AltermattII2006]. We use the incomplete ionization model of Altermatt et al. of References [AltermattI2006] and [AltermattII2006]. The relevant keywords and models are described in $impurity-parameters.
We use one Python script and use nextnanopy to generate the following figure.
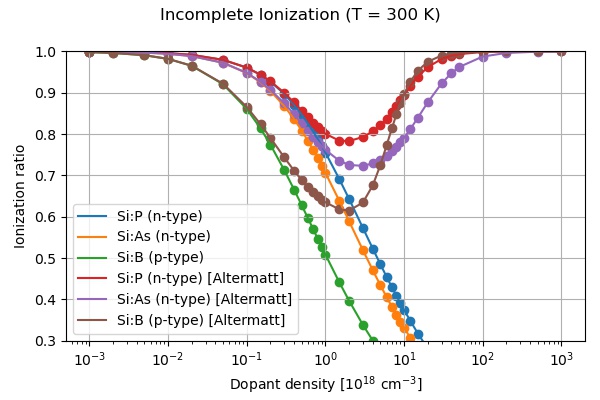
Figure 2.5.6 Ionization ratio of the donors P and As (n-type) and the acceptor B (p-type) in Si as a function of dopant density at room temperature. The figure compares our default model with the improved Altermatt model. At low dopant densities both models agree while for higher dopant densities the models differ substantially.
Our results differ from the original Altermatt paper. The minimum for Si:P (n-type) is close (~0.78 (nextnano) vs. ~0.76 (Altermatt)) while Si:As (n-type) differs more (~0.72 (nextnano) vs. ~0.66 (Altermatt)). The minimum for Si:B (p-type) also differs (~0.61 (nextnano) vs. ~0.73 (Altermatt)). It seems that Altermatt uses the Maxwell–Boltzmann approximation for the density in eq. (7) of [AltermattII2006] while our implementation is using Fermi–Dirac statistics based on his eqs. (5a) and (5b) of [AltermattII2006]. In fact, our model is not using his eqs. (6a), (6b) and (7), i.e. we are using the Fermi levels instead of the densities which might explain the discrepancy. It is not clear to us how his approach takes into account heavy holes, light holes and split-off holes as his eq. (7) indicates the usage of one type of holes only.
The parameters for the Altermatt model are specified as follows.
$doping-function doping-function-number = 1 impurity-number = 1 doping-concentration = 2.0 # 2.0 * [10^18 cm^-3] only-region = 0.0 20.0 # x_min x_max [nm] $end_doping-function $impurity-parameters impurity-number = 1 number-of-energy-levels = 1 impurity-type = n-type degeneracy-of-energy-levels = 2 energy-levels-relative = 0.0455 # n-P-in-Si [eV] ! [eV] incomplete-ionization-N-ref = 2.2 # 2.2 * 10^18 cm^-3 [10^18 cm^-3] incomplete-ionization-c = 2.0 # 2 [] incomplete-ionization-N-b = 6.0 # 6 * 10^18 cm^-3 [10^18 cm^-3] incomplete-ionization-d = 2.3 # 2.3 [] $end_impurity-parameters
If the 4 Altermatt specifiers (incomplete-ionization-N-ref, incomplete-ionization-c, incomplete-ionization-N-b, incomplete-ionization-d) are not present, the default model for incomplete ionization is used.

Figure 2.5.7 Ionization ratio of the donors P and As (n-type) and the acceptor B (p-type) in Si as a function of dopant density at T = 20 K. For low temperatures, only the Altermatt model leads to ionization at higher dopant densities.