Optical interband transitions in a quantum well - Matrix elements and selection rules

Input files:

• 1DQW_interband_matrixelements_finite_nnpp.in

• 1DQW_interband_matrixelements_infinite_nnpp.in

Scope:

We consider a 5 nm \(GaAs\) quantum well embedded between \(AlAs\) barriers. The structure is assumed to be unstrained. We distinguish between two cases:

1. finite \(AlAs\) barriers

2. infinite \(AlAs\) barriers (This can be achieved by choosing Dirichlet boundary conditions at the quantum well boundaries.)

Eigenstates and wave functions in the quantum well

a) Finite quantum well

Input file: 1DQW_interband_matrixelements_finite_nnpp.in

For finite barriers we obtain using single-band Schrödinger effective-mass approximation (i.e. isotropic and parabolic effective masses)

• 3 confined electron states in the Gamma conduction band (we do not consider L and X bands here)

• 5 confined heavy hole states

• 2 confined light hole states

• 3 confined split-off hole states

Figure 2.4.323 shows the band edges of the Gamma conduction band and the heavy, light and split-off hole band edges together with wave functions of the confined states. Note that the heavy and light hole band edge is degenerate.

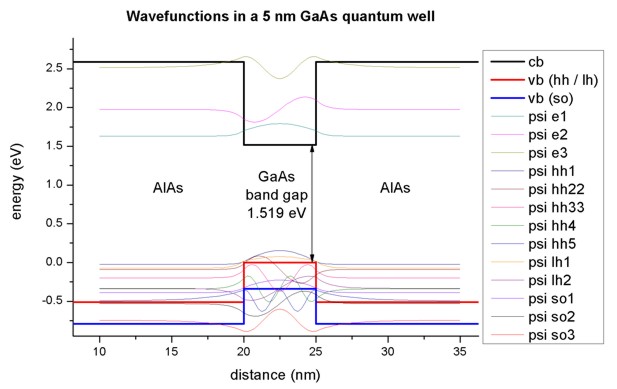
Figure 2.4.323 Calculated conduction band edge (black), hh/ lh valence bands (red) and split-off hole valence band (blue) with wave functions of lowest electron and hole states.

As one can see, the valence band looks rather messy. Thus, we zoom into it, see Figure 2.4.324 The 5 heavy hole wave functions are indicated in black, the 2 light hole wave function in red and the 3 split-off hole wave functions in blue.

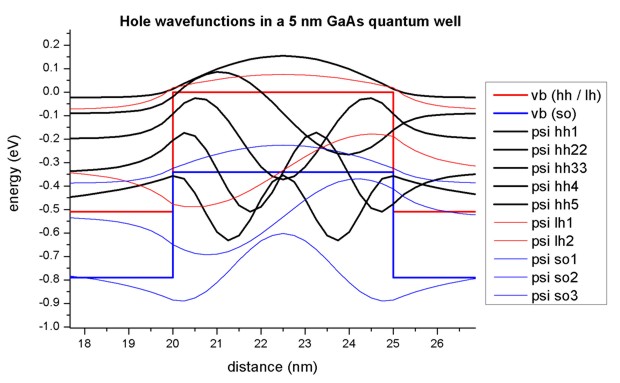
Figure 2.4.324 Calculated valence band edges and hole wave functions. The 5 heavy hole wave functions are indicated in black, the 2 light hole wave function in red and the 3 split-off hole wave functions in blue.

Interband matrix elements

Case b) Infinite quantum well

Input file: 1DQW_interband_matrixelements_infinite_nnpp.in

To understand the optical transitions we first examine the matrix elements of the envelope functions, i.e. the spatial overlap which is the integral over their product with no dependence on polarization:

\[\left\langle\psi_{\mathrm{cn}}|\psi_{\mathrm{vm}}\right\rangle = \delta_{\mathrm{nm}}\]

This leads to the so-called ‘Delta n = 0’ selection rule, i.e. only transitions between levels with the same index are allowed. Of course, this rule is not valid anymore for case a), where we have finite \(AlAs\) barriers, but nevertheless this rule gives the strongest transitions.

quantum{
    ...
    interband_matrix_elements{ # output matrix elements
        HH_Gamma{}
        LH_Gamma{}
        SO_Gamma{}
    }
}

The spatial overlap integrals of the envelope functions are contained in these files:

• bias_00000Quantuminterband_matrix_elements_quantum_region_HH_Gamma.txt - (heavy hole)

• bias_00000Quantuminterband_matrix_elements_quantum_region_LH_Gamma.txt - (light hole)

• bias_00000Quantuminterband_matrix_elements_quantum_region_SO_Gamma.txt - (split-off hole)

For instance, the matrix elements of the envelope functions for the ‘heavy hole’ to ‘conduction band’ transitions read:

Spatial overlap matrix elements < psi_hl_i | psi_el_j > and
                                       energy of transition in [eV].
heavy hole <-> Gamma conduction band
--------------------------------------------------------
<psi_vb001|psi_cb001>  1.001844         1.729371   ('Delta n = 0' selection rule)
<psi_vb001|psi_cb002>  3.456436E-016
<psi_vb001|psi_cb003>  7.866970E-016
<psi_vb002|psi_cb001>  7.463647E-016
<psi_vb002|psi_cb002>  1.007268         2.355209   ('Delta n = 0' selection rule)
<psi_vb002|psi_cb003>  2.844946E-016
<psi_vb003|psi_cb001>  9.575673E-016
<psi_vb003|psi_cb002>  1.450228E-015
<psi_vb003|psi_cb003>  1.015938         3.384106   ('Delta n = 0' selection rule)
<psi_vb004|psi_cb001>  1.076395E-015
<psi_vb004|psi_cb002>  1.422473E-015
<psi_vb004|psi_cb003>  2.019218E-015
<psi_vb005|psi_cb001>  1.960237E-016
<psi_vb005|psi_cb002>  1.346145E-015
<psi_vb005|psi_cb003>  1.217775E-015

The results shown above are for a 0.25 nm grid spacing (which is rather coarse). For a 0.1 nm grid spacing one obtains the following values for the relevant transitions:

<psi_vb001|psi_cb001>  1.000140         1.754633
<psi_vb002|psi_cb002>  1.000559         2.459675
<psi_vb003|psi_cb003>  1.001251         3.631886

Case a) finite quantum well

We now calculate the same matrix elements as above but this time for the finite \(AlAs\) barriers.

Spatial overlap matrix elements < psi_hl_i | psi_el_j > and
                                        energy of transition in [eV].
heavy hole <-> Gamma conduction band
-------------------------------------
<psi_vb001|psi_cb001>  0.987507         1.654103   ('Delta n = 0' selection rule)
<psi_vb001|psi_cb002>  1.336279E-014
<psi_vb001|psi_cb003>  0.145559         2.538366   (same parity: symmetric)
<psi_vb002|psi_cb001>  1.133344E-014
<psi_vb002|psi_cb002>  0.964789         2.065139   ('Delta n = 0' selection rule)
<psi_vb002|psi_cb003>  7.879180E-015
<psi_vb003|psi_cb001>  0.128041         1.829856   (same parity: symmetric)
<psi_vb003|psi_cb002>  4.286800E-015
<psi_vb003|psi_cb003>  0.839306         2.714118   ('Delta n = 0' selection rule)
<psi_vb004|psi_cb001>  6.263441E-015
<psi_vb004|psi_cb002>  0.215428         2.315853   (same parity: antisymmetric)
<psi_vb004|psi_cb003>  1.246759E-015

The results shown above are for a 0.25 nm grid spacing (which is rather coarse). For a 0.1 nm grid spacing one obtains the following values for the relevant transitions:

<psi_vb001|psi_cb001>  0.987955         1.652509
<psi_vb001|psi_cb003>  0.142978         2.541682
<psi_vb002|psi_cb002>  0.966524         2.062825
<psi_vb003|psi_cb001>  0.127100         1.828683
<psi_vb003|psi_cb003>  0.838394         2.717855
<psi_vb004|psi_cb002>  0.211786         2.317309

6-band k.p calculations for the infinite barrier \(AlAs\)/ \(GaAs\)/ \(AlAs\) quantum well

Input file: 1DQW_interband_matrixelements_infinite_kp_nnpp.in

Figure 2.4.325 shows the lowest 26 eigenstates obtained with 6-band k.p for the 5 nm \(GaAs\) quantum well with infinite barriers. Each k.p state is two-fold degenerate (spin up / spin down)

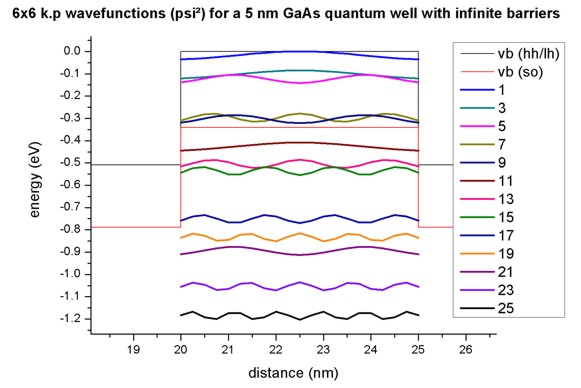
Figure 2.4.325 6-band k.p wave functions (\(Psi^2\)) for a 5 nm \(GaAs\) quantum well with finite barriers

One can easily relate the transitions to the ‘Delta n = 0’ selection rule. However, in contrast to the single-band approximation, the matrix elements are not necessarily equal to 1 anymore because the hole states are mixed and thus the hole envelope functions are significantly different to the electron envelope functions, even for an infinitely deep square well.

6-band k.p calculations for the finite barrier \(AlAs\)/ \(GaAs\)/ \(AlAs\) quantum well

Input file: 1DQW_interband_matrixelements_finite_kp_nnpp.in

Figure 2.4.326 shows the 6-band k.p hole wave functions for the quantum well having finite \(AlAs\) barriers. Their energies and \(Psi^2\) are two-fold degenerate due to spin but the wave functions \(\Psi\) are different! (not shown here). The electron wave functions (3 confined states) are the same as above.

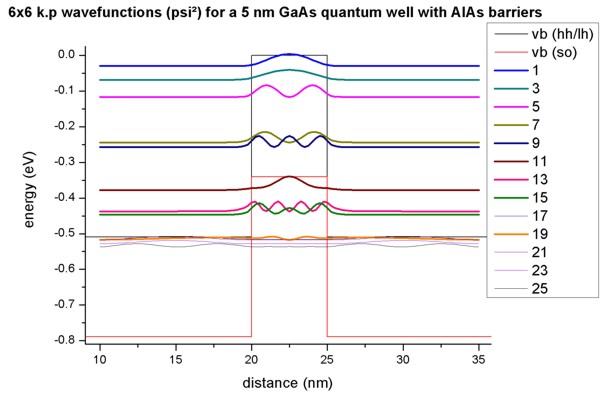
Figure 2.4.326 6-band k.p wave functions (\(Psi^2\)) for a 5 nm \(GaAs\) quantum well with \(AlAs\) barriers

The calculated spatial overlap integrals nicely show that in addition to the transitions where the ‘Delta n = 0’ selection rule is responsible, additional transitions arise due to symmetric/antisymmetric parity. All other transitions are zero. This is in agreement with the single-band results.

Last update: nn/nn/nnnn